前言
RSA算法是现今使用广泛的公钥密码算法,也是号称地球上最安全的加密算法。在了解RSA算法之前,先熟悉下几个术语
根据密钥的使用方法,可以将密码分为对称密码和公钥密码
对称密码:加密和解密使用同一种密钥的方式
公钥密码:加密和解密使用不同的密码的方式,因此公钥密码通常也称为非对称密码。
RSA算法原理
该部分转自http://blog.csdn.net/dbs1215/article/details/48953589
RSA加密
RSA的加密过程可以使用一个通式来表达,也就是说RSA加密是对明文的E次方后除以N后求余数的过程。

从通式可知,只要知道E和N任何人都可以进行RSA加密了,所以说E、N是RSA加密的密钥,也就是说E和N的组合就是公钥,我们用(E,N)来表示公钥
不过E和N不并不是随便什么数都可以的,它们都是经过严格的数学计算得出的,关于E和N拥有什么样的要求及其特性后面会讲到。顺便啰嗦一句E是加密(Encryption)的首字母,N是数字(Number)的首字母
RSA解密
RSA的解密过程也可以使用一个通式来表达,即对密文的D次方后除以N后求余数的过程。

这就是RSA解密过程。知道D和N就能进行解密密文了,所以D和N的组合就是私钥。

总结如下表:
生成秘钥对
既然公钥是(E,N),私钥是(D,N)所以密钥对即为(E,D,N)但密钥对是怎样生成的?
密钥对生成分求N、求L(L为中间过程的中间数,详见下文描述)、求E和求D以下几个步骤:
求N
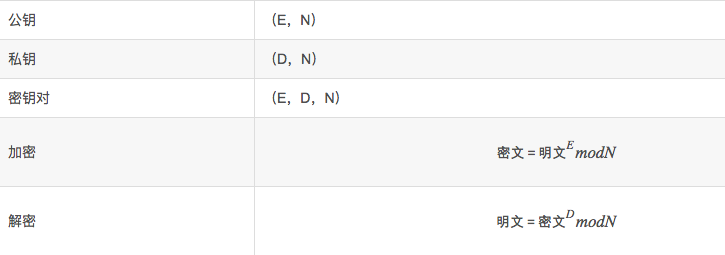
准备两个质数p,q。这两个数不能太小,太小则会容易破解,将p乘以q就是N
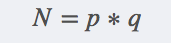
求L(L为中间过程的中间数)
L 是 p-1 和 q-1的最小公倍数,可用如下表达式表示:
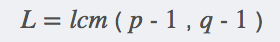
求E
E必须满足两个条件:E是一个比1大比L小的数,E和L的最大公约数为1
用gcd(X,Y)来表示X,Y的最大公约数则E条件如下:

之所以需要E和L的最大公约数为1是为了保证一定存在解密时需要使用的数D。现在我们已经求出了E和N也就是说我们已经生成了密钥对中的公钥了。
求D
数D是由数E计算出来的。D、E和L之间必须满足以下关系:
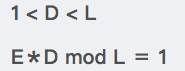
只要D满足上述2个条件,则通过E和N进行加密的密文就可以用D和N进行解密。
简单地说条件2是为了保证密文解密后的数据就是明文。
现在私钥自然也已经生成了,密钥对也就自然生成了。
生成秘钥对总结如下:

实践举例
5.1 求N
我们准备两个很小对质数,
p = 17
q = 19
N = p * q = 323
5.2 求L
L = lcm(p-1, q-1)= lcm(16,18) = 144
144为16和18对最小公倍数
5.3 求E
求E必须要满足2个条件:1 < E < L ,gcd(E,L)=1
即1 < E < 144,gcd(E,144) = 1
E和144互为质数,5显然满足上述2个条件
故E = 5
此时公钥=(E,N)= (5,323)
5.4 求D
求D也必须满足2个条件:1 < D < L,E*D mod L = 1
即1 < D < 144,5 * D mod 144 = 1
显然当D= 29 时满足上述两个条件
1 < 29 < 144
5*29 mod 144 = 145 mod 144 = 1
此时私钥=(D,N)=(29,323)
5.5 加密
准备的明文必须时小于N的数,因为加密或者解密都要mod N其结果必须小于N
假设明文 = 123
则 密文=明文EmodN=1235mod323=225
5.6 解密
明文=密文DmodN=22529mod323=123
解密后的明文为123。
一个直观的解释如下:
123的5次方mod323==Math.pow(123d, 5d) % 323d可以直接计算出是225;
再说5.6:
因为225的29次方数值太大,直接运算会导致取模结果获取错误结果;可以这样求解
(225的5次方mod323)==4;(225的4次方mod323)==290所以
225的29次方mod323==(225的5次方mod323)(225的5次方mod323)(225的5次方mod323)(225的5次方mod323)(225的5次方mod323)(225的4次方mod323) mod323==(4 4 4 4 290 4) % 323==123
RSA实现破解
RSA在软件逆向或加解密类的ctf题目中经常看到。在实际应用中,参数N和E是公开的但是D是私有的并且绝不能公开!两个大素数P和Q在生成密钥后便不再需要了,但是必须销毁,否则就可以推算出D。
为了从公钥(N,E)得到D,需要试图分解N为它的两个素数因子。对于一个很大的模数N(512位或更大)要想分解出它的P和Q是件非常困难的事。
ctf题目一
题目:给出密文flag.enc和公钥public.pem,解出密文
解题过程如下:
- openssl分析公钥,得到N,E
1
openssl rsa -pubin -text -modulus -in public.pem
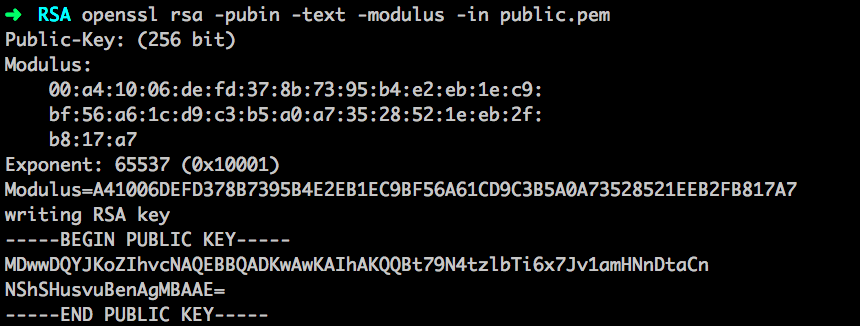
其中,Modulus 是n的值,Exponent是E的值。
- 使用msieve工具对N进行分解
1
msieve.exe 0xA41006DEFD378B7395B4E2EB1EC9BF56A61CD9C3B5A0A73528521EEB2FB817A7 -v
分解结果如下:
Msieve v. 1.53 (SVN 1005)
Wed Feb 28 23:00:33 2018
random seeds: f922db80 d61d4d18
factoring 74207624142945242263057035287110983967646020057307828709587969646701361764263 (77 digits)
searching for 15-digit factors
commencing quadratic sieve (77-digit input)
using multiplier of 7
using generic 32kb sieve core
sieve interval: 12 blocks of size 32768
processing polynomials in batches of 17
using a sieve bound of 921409 (36471 primes)
using large prime bound of 92140900 (26 bits)
using trial factoring cutoff of 26 bits
polynomial ‘A’ values have 10 factors
restarting with 19771 full and 188452 partial relations36803 relations (19771 full + 17032 combined from 188452 partial), need 36567
sieving complete, commencing postprocessing
begin with 208223 relations
reduce to 51729 relations in 2 passes
attempting to read 51729 relations
recovered 51729 relations
recovered 38607 polynomials
attempting to build 36803 cycles
found 36803 cycles in 1 passes
distribution of cycle lengths:
length 1 : 19771
length 2 : 17032
largest cycle: 2 relations
matrix is 36471 x 36803 (5.3 MB) with weight 1102159 (29.95/col)
sparse part has weight 1102159 (29.95/col)
filtering completed in 3 passes
matrix is 24858 x 24922 (4.0 MB) with weight 836197 (33.55/col)
sparse part has weight 836197 (33.55/col)
saving the first 48 matrix rows for later
matrix includes 64 packed rows
matrix is 24810 x 24922 (2.6 MB) with weight 611256 (24.53/col)
sparse part has weight 439905 (17.65/col)
commencing Lanczos iteration
memory use: 2.7 MB
lanczos halted after 394 iterations (dim = 24805)
recovered 14 nontrivial dependencies
p39 factor: 258631601377848992211685134376492365269
p39 factor: 286924040788547268861394901519826758027
elapsed time 00:00:06
两个p39 factor为p和q,这里是10进制表示
- 生成私钥
知道了N,e,p,q,就可以生成私钥了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24import math
import sys
from Crypto.PublicKey import RSA
keypair = RSA.generate(1024)
keypair.p = 0xD7DB8F68BCEC6D7684B37201385D298B
keypair.q = 0xC292A272E8339B145D9DF674B9A875D5
keypair.e = 65537
keypair.n = keypair.p * keypair.q
Qn = long((keypair.p-1) * (keypair.q-1))
i = 1
while (True):
x = (Qn * i ) + 1
if (x % keypair.e == 0):
keypair.d = x / keypair.e
break
i += 1
private = open('private.pem','w')
private.write(keypair.exportKey())
private.close()
注:生成的私钥会默认base64加密。
密钥解密密文1
2
3openssl rsautl -decrypt -in flag.enc -inkey private.pem -out flag.txt
cat flag.txt
ISG{256bit_is_weak}
附:
常用工具下载地址
RSA-tool 2 http://www.skycn.net/soft/appid/39911.html